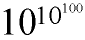Hamlet is a Big Number
 Yes, all Shakespeare did when he wrote Hamlet is choose a number; a really big number. He chose a literary number, as I describe below. The fact that he was able to choose one to stir the emotions of billions of souls was due to his being a human rather than a monkey typing away randomly at a typewriter. But still the monkey's gibberish and Hamlet come from the same number domain.
Numbers come in six different size domains. These determine how we use the numbers. How big are the numbers we use? Can you count to 400? Can you count to a billion? Can the national debt be a googol dollars (a googol is 1 followed by a hundred zeros)? The answers are yes, no and no. This is because we use numbers out of their domain. One can count to 400 because 400 is a counting number, but not to a billion because a billion is in the next domain, the statistical numbers. This means that a budgetary item can be billions of dollars but not googols of dollars, as googol is in the next domain, the scientific numbers. The six domains are:
Yes, all Shakespeare did when he wrote Hamlet is choose a number; a really big number. He chose a literary number, as I describe below. The fact that he was able to choose one to stir the emotions of billions of souls was due to his being a human rather than a monkey typing away randomly at a typewriter. But still the monkey's gibberish and Hamlet come from the same number domain.
Numbers come in six different size domains. These determine how we use the numbers. How big are the numbers we use? Can you count to 400? Can you count to a billion? Can the national debt be a googol dollars (a googol is 1 followed by a hundred zeros)? The answers are yes, no and no. This is because we use numbers out of their domain. One can count to 400 because 400 is a counting number, but not to a billion because a billion is in the next domain, the statistical numbers. This means that a budgetary item can be billions of dollars but not googols of dollars, as googol is in the next domain, the scientific numbers. The six domains are:
1. Counting numbers.
Also lottery numbers, gambling numbers, discrete numbers. These are numbers you can count to. They range from zero to about 1,000 or so. We use these numbers to enumerate quantities that we think of in discrete terms. There are seven days in the week, 43 people in the building, and so forth. We can conceive these easily in our mind either directly (4) or through patterns (361 - a 19 x 19 square). There are not many of these numbers, and they, especially the lower ones, tend to acquire a supernatural significance. For example, astrology evolved with 12 signs, rather than, say, with 32,768 signs. In the same way, people gamble with these and bet on a seven coming up on dice or on a certain bingo number coming up. People can lose their fortunes on these numbers.
2. Statistical numbers.
Also budget numbers, human numbers, mass numbers. These are the numbers that most frequently appear as statistics in almanacs. For example, Richmond, Virginia has 202,798 people, and world petroleum reserves are about 1 trillion barrels. Statistical numbers range from 1,000 to about a quadrillion (1,000,000,000,000,000) or so. Trillions are commonly used in our society but not quadrillions. Like counting numbers, these are frequently misused, as in "millions have been successful in using this product.", even though this is only about 0.5% of the total population.
3. Scientific Numbers.
Ranging from a quadrillion to a little over a googol, these numbers are seen mainly in science. It is no coincidence that the notation 6.023E23 (Avogadro's number) for a number, meaning 6.023 times 10 to the 23rd power, is called scientific notation. These numbers describe the number of grains of sand on a beach, the number of atoms in our bodies and in the Earth, and the number of years for a solar-sized black hole to explode (1 followed by 66 zeroes). There are names for these numbers, such as quadrillion, decillion, and vigintillion, but these names are rarely used. We encounter these numbers rarely, but they describe our universe and its size.
4. Literary numbers.
Literary numbers can be as small as about a googol or as large as 1 followed by tens of billions of zeroes. Now the numbers are so big that they can't describe phenomena in the universe. The decimal expansions of these numbers fill pages of paper, as do text in books. Examples of these numbers are 2 to the 65536 power and Shakespeare's Hamlet. If one uses base 35 instead of ten, with a = 0, b = 1, ..., z = 25, . = 26, , = 27 , space = 28 and so forth, then Hamlet can be regarded as a representation of a huge number, with tens of thousands of digits. Since literary works can be thought of as numbers of this magnitude, I call them literary numbers. Just think that when a writer produces a masterpiece such as Hamlet, War and Peace, and so forth, he is merely selecting one of these numbers. Your computer's disk drive is a sequence of binary digits; hence a literary number. Any time you do something on your computer, you change this number. If your disk drive is 10 GB, then it expresses a number somewhere around one followed by ten billion zeroes.
Most of these numbers can be written down, understood, or conceived. However, when there are tens of billions of digits or more, that begins to exceed the ability of the human mind to comprehend it. There are only 20 billion instants (an instant is a tenth of a second) in our lifetimes.
5. Inconceivable numbers.
That brings us to the inconceivable numbers, larger than 1 followed by 20 billion zeroes or so. These numbers can no longer describe literary works. A googolplex is one followed by a googol zeroes. A googol letters is far more than the printed literary works of all humankind over all time. We can't conceive most of these numbers because most can be described no better than to simply write down all their digits. Note that some of these numbers can be described; for example, a googolplex is
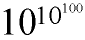
so can be written down in seven symbols. But a googolplex is larger than many numbers of a googol digits which can't be described by us since it requires writing a googol digits down. So a googolplex, larger than these numbers, is also inconceivable. Inconceivable numbers can be really huge; so huge that knowledge of transfinite ordinal numbers is needed to understand how big they are.
6. Indescribable numbers.
Finally there are indescribable numbers. These numbers are larger than the largest number we will ever be able to describe with our finite resources. They are incredibly huge and obviously I can't give any examples.
There you have it - the six domains of numbers. All the way from numbers you can count with to numbers that can describe you. Hope your numbers are all propitious.
Jim Blowers, Ph.D
Back to Main Page