My congregation, the First Unitarian Church of Richmond, has an interesting program called Sip 'n Sup. The purpose of this group is to get people of the church more acquainted with each other. For five evenings during the winter and spring, the members agree to host each other for dinner. Most members are couples, but some are singles or pairs of single people. Each dinner consists of five couples, or usually ten people. It is held at the home of one of the couples. That couple prepares the dinner for all five of the couples.
Since the purpose is to get everyone introduced to each other, the program is set up so that at each dinner each couple encounters a set of other couples completely different from any of the other dinners. Hence any two dinners have only one couple in common. Everyone is required to host exactly once in the program. To the extent possible, everyone goes to a dinner on each of the five nights.
A sample schedule follows:
2000/01/03
Yancey Valentine Miller Kelley Ginger
Smith Quinton Ferguson Johnson Donaldson
Robertson Paulson Burnham Orenson Ianna
Nathanson Wesley Lang Houston Zweibel
Eggleston Trenton Cox Underwood Anton
2000/02/04
Ginger Smith Underwood Lang Paulson
Donaldson Robertson Kelley Cox Wesley
Ianna Nathanson Johnson Miller Trenton
Zweibel Eggleston Orenson Ferguson Valentine
Anton Yancey Houston Burnham Quinton
2000/03/03
Kelley Nathanson Paulson Ferguson Anton
Johnson Eggleston Wesley Burnham Ginger
Orenson Yancey Trenton Lang Donaldson
Houston Smith Valentine Cox Ianna
Underwood Robertson Quinton Miller Zweibel
2000/04/06
Miller Smith Wesley Orenson Anton
Ferguson Robertson Trenton Houston Ginger
Burnham Nathanson Valentine Underwood Donaldson
Lang Eggleston Quinton Kelley Ianna
Cox Yancey Paulson Johnson Zweibel
2000/05/01
Wesley Yancey Underwood Ferguson Ianna
Burnham Smith Trenton Kelley Zweibel
Valentine Robertson Johnson Lang Anton
Quinton Nathanson Orenson Cox Ginger
Paulson Eggleston Houston Miller Donaldson
The bold face indicates the hosts. Some questions to be answered are: How does one schedule a Sip 'n Sup program? How do you come up with a scheduling scheme like this?
One way of finding mathematical truth is to find metaphors for the problem you are working on. In the case of Sip 'n Sup, the main property is that each pair of couples meets each other only once. For example, the Fergusons and Quintons meet only once, on January 3. What about dinners? If you pick two dinners, it seems then there is one and exactly one couple between them. For example, the third dinner on March 3 and the second dinner on April 6 have the Trentons and only the Trentons in common. Of course these maxims don't always hold. The Zweibels and the Donaldsons never meet each other, but notice that they happen to host two different dinners the same night. If you check the schedule, you find that if any two couples host on the same night, they never meet each other, but if they host on different nights, then they meet some time. And obviously, two dinners can't intersect in any couples if they happen to be scheduled on the same night, for no one can be in two different places at the same time.
So in what other areas do two things come together into one point? Set theory is a possibility. We can talk of intersecting two dinners, for example, and getting a single couple, or no couple if they are the same night. But intersection brings another possible analogy to mind: geometry. Recall that two of Euclid's axioms are:
Let's then schedule a Sip 'n Sup for all the points in the Euclidean plane. We need analogies for all the essential parts of a Sip 'n Sup. The points are couples, for instance. What are the dinners? They are the lines. Each line consists of a set of points in the plane, and we can imagine all these points meeting each other for dinner. In that case, if you have two points A and B, that determines a line and hence a dinner:

So every pair of couples meets only once for dinner. If two lines L and M are given, then if they intersect, then the couple-point in common, A, will go to both line-dinners: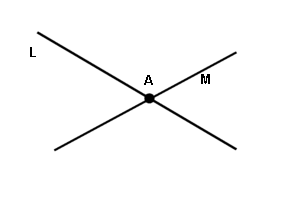
Further, that is the only point in both lines that will be at both of these dinners.
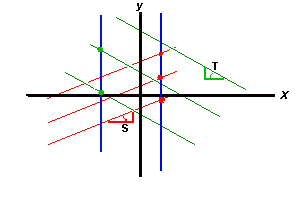
The red lines represent one family S of parallel lines. They have the same slope as indicated by the red triangle. The green lines T represent another family, this time with a negative slope. Both of these then are Sip 'n Sup nights. But then who hosts these nights? A method is needed of associating to each line/dinner on a night based on the slope of that night a unique point on that night to host the dinner. Recall that each line in the plane can be represented as an equation y = mx + b, where m is the slope and b is the y-intercept, the place where the line intersects the vertical y-axis. So all the lines that are held on the same night have the same slope. Note also that one family of parallel lines has no slope: the vertical family. Each line in each of the other families of lines (nights) intersects each line of the vertical line family in a unique point. So one way of choosing a host for the dinner is to choose this point. For example, the vertical line on the right in the diagram might have its x value equal to the slope of the red lines. If so, then the red dots represent the points that host those dinner lines. Similarly, the blue vertical line to the left of the vertical axis may represent the slope of the green lines; if so, then the hosts for these dinners are marked by the green dots.
The vertical lines can't be dinners, as they intersect all other dinners and so these couples would be attending those other dinners. Instead, they are host sets. In the Sip 'n Sup schedule above, note that the schedule is formed by taking the sets of hosts for a given night and rotating them around. These sets of hosts will never meet each other. This is hard to see from the schedule above, but the geometrical analogy makes it clear: the host sets don't meet each other because they are parallel lines.So now we can schedule our Sip 'n Sup. We imagine that there is a day for each point on the real line. This would be hard to construct, as there are an uncountable infinity of points, so that they can't be strung out in finitely long days. But just imagine. On day n, the lines of slope n are the dinners, and the hosts for these dinners are the points on these lines whose x value is n; i.e., where the line intersects the vertical line x = n.
OK, what good is this? We don't have an uncountable infinity of people in our group. Maybe we have 25 people instead. We need to do geometry for 25 points instead of an infinity of them. There is a way of doing that. Note that Euclidean geometry is based on the arithmetic of the real numbers, which I shall call R. Each point is assigned a pair of real numbers; its coordinates. In expressing a line as an equation y = mx + b. We need addition and multiplication to construct this equation, and to work with it, we need subtraction and division too; for example, x = (y-b)/m. A mathematical universe in which one can perform all four of these operations in the usual manner is called a field. R is a field.
But R is not the only field. Another field can be constructed out of the integers, by taking their remainders upon division by 5. This results in an arithmetic called arithmetic modulo 5, with only five elements. For example, 2 + 1 = 3, but 2 + 4 = 1, since we throw out 5 out of the 6 thar results from 2 + 4. This means that 1/2 = 3, because 2 x 3 = 1, and so forth. You can do all sorts of arithmetic in this tiny five-member universe of {0, 1, 2, 3, 4} except division by zero. Therefore, this arithmetic is a field. It is usually denoted Z5.
So why not do geometry in this field? Set up our parallel lines and slopes just as with R, but do it in Z5 instead. Since lines have 5 points in them (the number of elements of Z5), the plane will have 25 points, so it can be represented as a table. The top row indicates the x values of the cells, and hence the slopes of the night families:
| 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| 0 | ||||
|---|---|---|---|---|
| Host | ||||
| Host | ||||
| Host | ||||
| Host | ||||
| Host |
| 4 | ||||
|---|---|---|---|---|
| Host | ||||
| Host | ||||
| Host | ||||
| Host | ||||
| Host |
On Night 3 we can take the lines diagonal upward. This means a slope of 1; that's the second column. So now the second column hosts:
| 1 | ||||
|---|---|---|---|---|
| Host | ||||
| Host | ||||
| Host | ||||
| Host | ||||
| Host |
| 2 | ||||
|---|---|---|---|---|
| Host | ||||
| Host | ||||
| Host | ||||
| Host | ||||
| Host |
| 3 | ||||
|---|---|---|---|---|
| Host | ||||
| Host | ||||
| Host | ||||
| Host | ||||
| Host |
| 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Yancey | Ginger | Kelley | Miller | Valentine |
| Smith | Donaldson | Johnson | Ferguson | Quinton |
| Robertson | Ianna | Orenson | Burnham | Paulson |
| Nathanson | Zweibel | Houston | Lang | Wesley |
| Eggleston | Anton | Underwood | Cox | Trenton |
So what if 30 people or 36 sign up for your Sip N Sup? First of all, you don't have to use all of the columns for your Sip 'n Sup Schedule. For 35 participants, the best way is to use a schedule based on Z7, using a 7x7 square, and omit the last two columns from each dinner. There will be people who don't host the same night who don't meet each other either, but at least people won't repeat seeing other faces. They will meet as many people as they can. The ideal number of people for a dinner seems to be 10 (5 couples), but 8 (4 couples) will work as well. Even for 30 people, omit the last two columns and part of the third one. This means a lot of four-couple dinners but that is probably acceptable. If you want to know how to schedule a specific number of people for your Sip 'n Sup, then contact me at jimvb@mindspring.com
So properties of geometrical figures such as points and lines help determine how to get a group of people unfamiliar to get to know each other through Sip and Sup. If you are a member of a large group such as a church, try it and see how it works.
Jim Blowers, Ph.D. 2002 May 5 Back to main page